СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
ГЛАВА I. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. 7
1.1. Общая характеристика задачи линейного. 8
программирования. 8
1.2. Математическая постановка задачи линейного. 8
программирования. 8
ГЛАВА II. ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. 11
2.1 Математическая постановка транспортной задачи. 11
2.2. Решения транспортной задачи с помощью программы Ms Excel 13
2.3. Решение транспортной задачи с помощью методов. 18
потенциалов. 18
2.4. Рекомендации по решению задач оптимизации с помощью надстройки Поиск решения. 29
ГЛАВА III. ДВОЙСТВЕННАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. 36
3.1 Математическая формулировка двойственной задачи. 36
линейного программирования. 36
3.2 Математическая постановка двойственной задачи о красках. 37
3.3 Решение двойственной задачи о красках с помощью MS Exsel 37
СПИСОК ЛИТЕРАТУРЫ.. 42
ГЛАВА I. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
1.2. Математическая постановка задачи линейного программирования.
В общем случае математическая постановка задачи линейного программирования, может быть сформулирована в следующем виде:
f(x1,x2…,,x n)® где (1.1)
x1,x2…,,x n (1.2)
(k{1,2,…,m}).
при этом следует принимать во внимание следующие принципиальные предположения о характере целевой функции и левых частей ограничений:
- Целевая функция f(x1,x2…,,x n) предполагается линейной относительно всех своих переменных, т.е. может быть представлена в форме всех своих представлена в форме: f(x1,x…,,x n)=с1х1+с2х2+…+с nx n.
- Левые части ограничений g k(x1,x2…,,x n) ({1,2,…,m}) также является линейными функциями относительно своих переменных x1,x2…,,x n, т.е. могут быть представлены в форме: g k(x1,x2…,,x n)=ак1х+ак2х2+…+а к nx n.
- Переменные x1,x2…,,x n могут принимать свои значения только из множество неотрицательных действительных чисел R1+ ,т.е. хi R1+ ({1,2,…,n}).
С учетом сделанных предположений общая задача линейного программирования может быть сформулирована следующим образом.
Необходимо найти максимум линейной целевой функции n переменных x1,x2…,,x n R1+ следующего вида: ...
ГЛАВА II. ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
2.2. Решения транспортной задачи с помощью программы Ms Excel
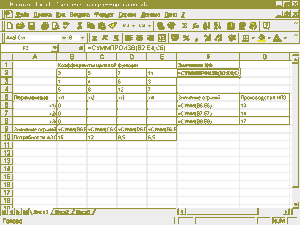
Рисунок. 2.1 Исходные данные для решения транспортной задач
... Результатом решения транспортной задачи являются найденные оптимальные значения переменных: х11=0, х12=1,5, х13=8,5, х14=0, х21=14, х22=0, х23=0, х24=0, х31=1, х32=10,5, х33=0, х34=5,5, которым соответствует значение целевой функции: f opt= 208,5. При выполнении расчетов для ячеек В6:Е8 был выбран числовой формат с тремя знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения потребностей АЗС №1 следует транспортировать 14т бензина из НПЗ №2 и 1т- из НПЗ №3, для удовлетворения потребностей АЗС №2 следует транспортировать 1,5 т бензина из НПЗ №1 и 10,5т – из НПЗ №3, для удовлетворения потребностей АЗС №3 следует транспортировать 8,5 т бензина из НПЗ №1 и, наконец, для удовлетворения потребностей АЗС №4 следует транспортировать 5,5 т бензина из НПЗ №3. При этом общая стоимость найденного плана перевозок составит 208,5 тысяч тенге. ...
ГЛАВА III. ДВОЙСТВЕННАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ.
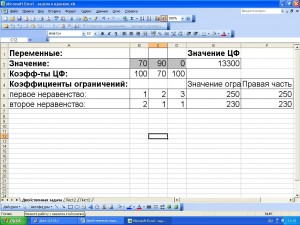
Рисунок 3.4. Отчет по результатам.
... Применительно к паре решенных двойственных задач (4.3.1) и (4.3.2) и (3.3) и (3.4) первые два неравенства прямой задачи (4.3.2) превращаются в равенства, откуда следует, что запасы индиго и железного купороса используются полностью. Об этом свидетельствуют и оптимальные значения двойственных переменных: у1=70, у2=90. Напротив, запасы свежегашеной извести используются не полностью, что согласуется со значением третьей двойственной переменной найденного оптимального решения у3=0.
Для целей экономического анализа модели задачи линейного программирования удобно предположить, что двойственные переменные могут выступать в роли оценок типов сырья, используемого в производстве красок. Более того, величина данной двойственной оценки показывает, на сколько возрастет максимальное значение целевой функции прямой задачи при увеличении количества сырья соответствующего типа на 1кг.
Таким образом, двойственные оценки могут быть использованы для определения степени дефицитности типов сырья для производства продукции. В связи с этим анализ оптимальных решений прямой и двойственных задач линейного программирования становится необходимым этапом экономического анализа эффективного планирования производства продукции. ...